백준 18352번 - '특정 거리의 도시 찾기'

---

18352번: 특정 거리의 도시 찾기

1. 문제

1번 부터 N번 까지의 도시가 M개의 단방향 도로가 존재 합니다. 모든 도로의 거리는 1로 같습니다. 이 때 X번 도시 부터 출발 하여 최단 거리가 K인 모든 도시들의 번호를 출력하는 프로그램을 작성 하시오. (2 <= N <= 300,000, 1 <= M <= 1,000,000, 1 <= K <= 300,000, 1<= X <= N)

 

 

2. BFS - 최단거리 / 최단경로

'최단 거리' 단어에서 BFS(너비 우선 탐색) 으로 접근 할수 있을거 같습니다. 왜냐하면, 가장 먼저 삽입한 노드를 가장 먼저 꺼내야 하는 자료구조를 사용해야 최단 거리를 구할 수 있습니다. 이러한 자료구조는 큐가 존재 합니다. 큐는 선입선출(FIFO)로 동작 합니다. DFS는 스택을 사용하고, BFS는 큐 자료구조를 사용 합니다. 따라서, '최단 경로', '최단 거리' 같은 용어가 쓰였다면, BFS를 의심해 봐야 합니다.

 

 

3. BFS - 자료구조에 따른 시간 복잡도

그리고 노드와 엣지를 표현하는 자료구조도 신경을 써야 합니다. 이 자료구조와 무방향 그래프/단방향 그래프에 따라서 시간 복잡도와 공간 복잡도가 달라집니다.

 

 

bfs는 노드와 엣지의 정보를 표현한 자료구조를 모두 탐색하기 때문에 시간 복잡도는 노드와 엣지의 정보를 표현한 자료구조에 따라서 시간 복잡도와 공간 복잡도가 달라집니다. dfs도 아래와 같은 시간복잡도와 공간복잡도를 따릅니다.

 

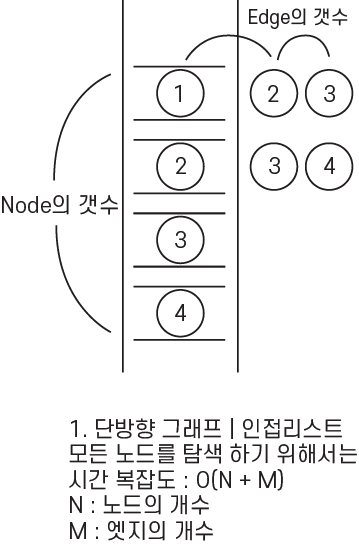
1. 단방향 그래프 | 인접리스트

단방향 그래프를 인접 리스트로 표현하는 경우에는 위 그림과 같이 단방향 이므로 하나의 서브 리스트에는 중복되는 노드가 담기지 않습니다. 따라서, 이 인접 리스트를 모두 탐색하려면, 시간 복잡도 : O(N + M), 공간 복잡도 : O(N + M) 이 소요 됩니다.

 

2. 무방향 그래프 | 인접리스트

무방향 그래프를 인접 리스트로 표현 하는 경우에는 노드와 노드 사이의 방향이 없으므로 하나의 서브 리스트에 중복 되는 노드가 포함 됩니다. 따라서, 시간 복잡도 :  O(M + M), 공간 복잡도 : O(M + M)가 소요 됩니다.

 

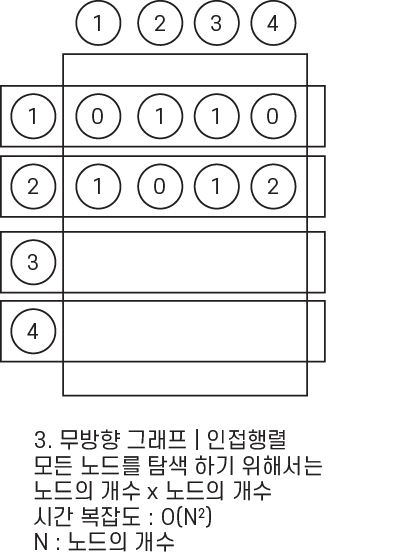
3. 무방향 그래프 | 인접행렬

무방향 그래프를 인접 행렬로 표현하는 경우에는 모든 노드를 2차원 배열로 표현 하고, 해당원소를 0 또는 1로 표현하거나 비용으로 표현 합니다. 따라서, 시간 복잡도 : O(N x N), 공간 복잡도 : O(N x N)가 소요 됩니다.

 

 

2. 문제 접근 

1. 먼저, 도시와 도로 정보를 담는 자료구조를 선정해야 합니다.

2. 출발 도시를 인덱스로 하고, 도착 도시를 원소로 갖는 List<List<Integer>> 형태의 인접리스트로 도시와 도로 정보를 초기화 시켜 줍니다.(단방향 그래프 | 인접리스트)

2. 시작 도시의 번호를 큐의 삽입 합니다.

3. 큐의 원소가 텅 빌 때 까지 반복 합니다.

4. 큐에서 가장 먼저 삽입한 원소를 꺼냅니다.

5. 현재 원소의 인접 노드(도시)를 돌면서, 아직 방문 하지 않은 원소라면, 해당 원소의 거리값을 이전 원소(Predecessor)의 거리값 + 1(도시와 도시 사이의 거리)을 할당 합니다.

6. 그리고 해당 원소를 큐의 삽입 하고, 방문 처리 합니다.

7. 큐의 원소가 빌 때 까지 순환 후

8. 도시들의 최단 거리 배열에서 문제에서 찾는 최단 거리 K와 같은 값이 있다면, 출력해 줍니다. 

 

 

3. java 소스 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class BOJ18352 {
    // https://www.acmicpc.net/problem/18352
    // 특정 거리의 도시 찾기
    public static void main(String[] args) throws IOException {
        // x 번 도시 부터 출발
        // k 번 이동 하였을 때 도시 출력
        // 만약, k번 이동 전에 경유 하는 도시는 제외
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        // 도시의 개수
        int n = Integer.parseInt(st.nextToken());
        // 도로의 개수
        int m = Integer.parseInt(st.nextToken());
        // 거리 정보 k
        int k = Integer.parseInt(st.nextToken());
        // 출발 도시 번호
        int x = Integer.parseInt(st.nextToken());

        // roadInfos(인접리스트) 초기화
        List<List<Integer>> roadInfos = new ArrayList<List<Integer>>();
        for (int i = 0; i < n + 1; i++) {
            List<Integer> roadInfo = new ArrayList<>();
            roadInfos.add(roadInfo);
        }

        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            roadInfos.get(a).add(b);
        }

        CityFinder cityFinder = new CityFinder(roadInfos, n, k);
        List<Integer> lookingForCity = cityFinder.find(x);

        printLookingForCity(lookingForCity);
    }

    // 찾은 도시 출력, 없으면 -1 출력
    public static void printLookingForCity(List<Integer> lookingForCity) {
        final int NONE = -1;

        if (lookingForCity.isEmpty()) {
            System.out.println(NONE);
        } else {
            for (Integer integer : lookingForCity)
                System.out.println(integer);
        }
    }
}

class CityFinder {

    private List<List<Integer>> roadInfos;
    private List<Integer> lookingForCity;
    private int[] distances;
    private Queue<Integer> queue;
    private int moveCnt;

    public CityFinder(List<List<Integer>> roadInfos, int n, int k) {
        this.roadInfos = roadInfos;
        this.lookingForCity = new ArrayList<>();
        this.distances = new int[n + 1];
        this.queue = new LinkedList<>();
        this.moveCnt = k;
    }

    public List<Integer> find(int startCity) {
        // bfs로 최단 거리 배열(distances[])를 구한다.
        bfs(startCity);
        
        // 거리 K의 최단 거리 도시를 결과 배열에 담는다.
        addCityThatIsTargetDistance();
        
        return lookingForCity;
    }

    private void bfs(int startCity) {
       queue.offer(startCity);

        while (!queue.isEmpty()) {
            int cur = queue.poll();
            List<Integer> nextCitys = roadInfos.get(cur);

            // 현재 도시 기준으로, 인접한 도시들 순회 한다.
            for (Integer nextCity : nextCitys) {
                // 방문 하지 않은 도시 라면
                if (distances[nextCity] == 0) {
                    // 다음 도시 = 현재 도시까지의 최단 거리 + 1
                    distances[nextCity] = distances[cur] + 1;
                    // 큐에 다음 도시 번호를 삽입 한다.
                    queue.offer(nextCity);
                }
            }
        }
    }

    private void addCityThatIsTargetDistance() {
        int i = 0;
        for (int distance : distances) {
            if (moveCnt == distance) {
                lookingForCity.add(i);
            }
            i++;
        }
    }
}

여기서, 최대 N : 300,000, M : 1,000,000 이고, 단방향그래프 | 인접리스트 이므로, 시간복잡도, 공간복잡도 : O(N + M) = 1,300,000 입니다.

 

 

4. 문제 접근2

이 문제에서 최단거리를 구하기 위해서, 왜 DFS가 아닌 BFS를 사용 하는지 좀더 자세하게 알아 보겠습니다. 위 그림과 같은, 입력을 예시로 표현해 보겠습니다.

 

 

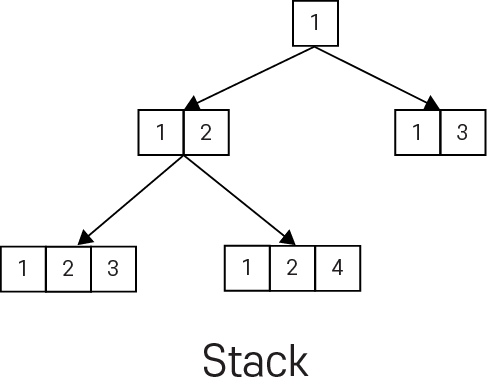
먼저, 스택과 큐로 데이터의 접근을 표현하면 위와 같이 표현 할 수 있습니다. 그림은 스택과 큐 모두 동일해 보입니다. 하지만, 진행 순서에서 차이가 납니다. 

 

 

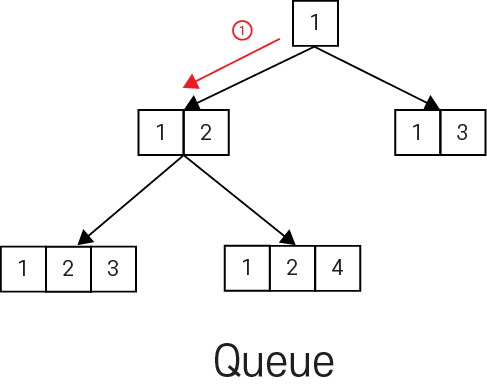
1. 첫번째 진행은 둘다 같습니다.

 

 

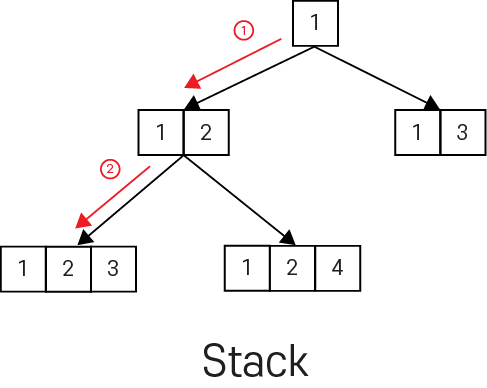
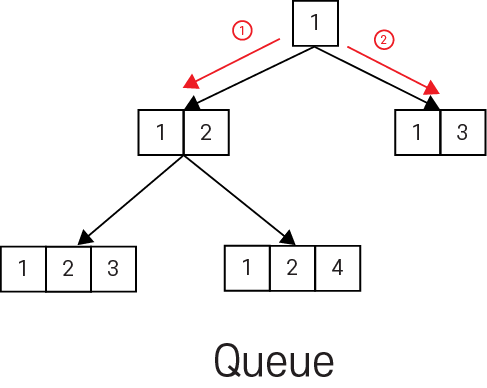
2. 여기서, 가장 차이가 많이 납니다. 스택의 경우에는 그 다음 depth로 진행하고, 큐에 경우에는 그 다음 depth가 아니고 현재 depth를 모두 탐색 합니다. dfs와 bfs에서 모두 방문 체크를 하게 되는데, 스택의 경우에는 1번 -> 3번으로 가는 최장 경로를 먼저 탐색 하고, 방문 체크를 합니다. 하지만, 큐에 경우에는 1번 -> 3번으로 가는 최단 경로를 먼저 탐색 하고, 방문 체크를 합니다. 따라서, 스택은 1번 -> 3번으로 가는 최장경로에서 방문 체크를 하였기 때문에, 추후에 1번 -> 3번에 최단 경로를 탐색 하였어도, 최단 경로를 찾기 어렵습니다. 반면, 큐는 최단 경로 부터 찾아내기 때문에, '최단 거리', '최단 경로' 문제에서는 bfs를 의심해야 합니다. 

 

 

 

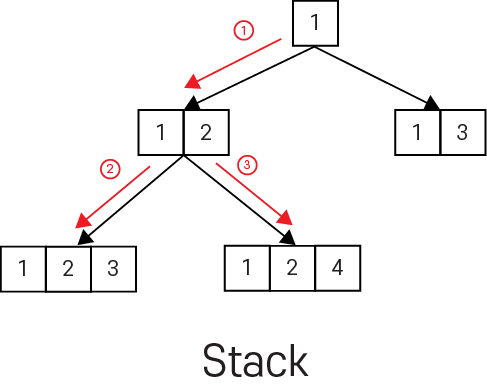
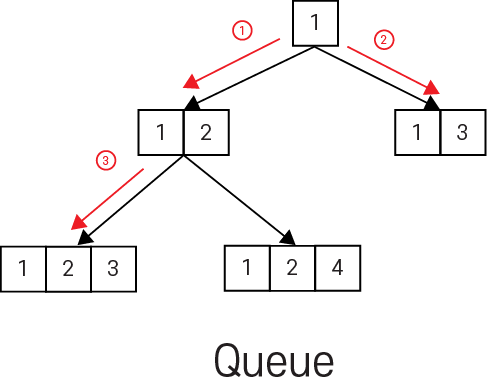
3. 위와 같이 진행 합니다.

 

 

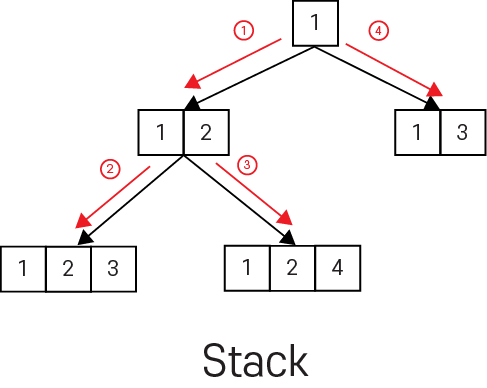
4. 위와 같이 진행 합니다.