합병 정렬 (Merge Sort)

Merge Sort, Quick Sort, Heap Sort 중 에서 Merge Sort, Quick Sort 는 분할 정복법 (Divide and Conquer) 에 해당 합니다.
* 분할 정복법
- 분할 : 해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할
- 정복 : 각각의 작은 문제를 순환적으로 해결
- 합병 : 작은 문제의 해를 합하여(merge) 원래 문제에 대한 해를 구함
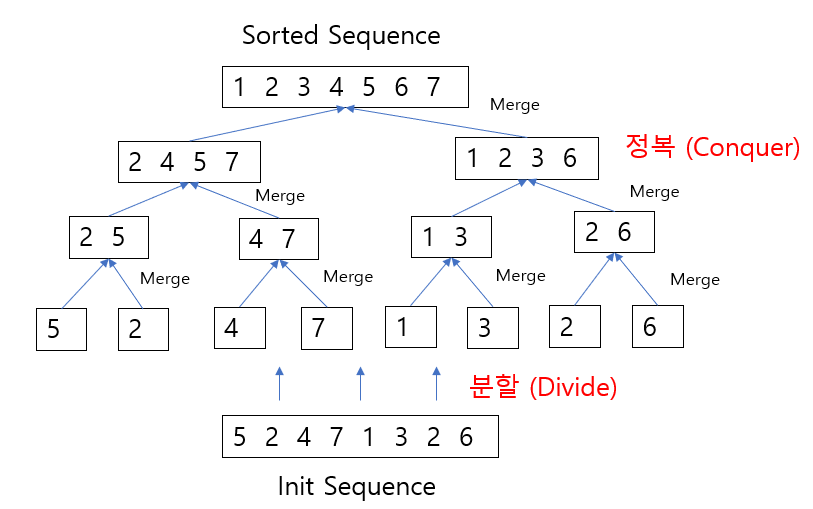
1. Merge Sort 는 위 그림과 같이 주어진 배열을 분할 해줍니다.
(5, 2)
(4, 7)
(1, 3)
(2, 6)
2개의 원소들로 분할 해줍니다.
2. 분할된 각 원소들을 각각 정렬(합병) 시켜 줍니다.
(5), (2) -> 정렬 -> (2, 5)
(4), (7) -> 정렬 -> (4, 7)
(1), (3) -> 정렬 -> (1, 3)
(2), (6) -> 정렬 -> (2, 6)
3. 2번 과정을 반복 합니다.
정렬된 (2, 5), (4, 7) -> 정렬 -> (2, 4, 5, 7)
아래와 같이 정렬 해줍니다.

이와 같은 방법으로 (1, 3), (2, 6) -> (1, 2, 3, 6)으로 정렬 해줍니다.
4. 마찬가지로 3번과 같은 방법으로
(2, 4, 5, 7), (1, 2, 3, 6) -> (1, 2, 3, 4, 5, 6, 7)로 정렬 해줍니다.
* sudo 코드

* merge 함수 구현
void merge(int[] data, int p, int q, int r) {
int[] tmp = new int[data.length];
// 전반부 인덱스
int i = p;
// 후반부 인덱스
int j = q + 1;
// tmp 배열의 인덱스
int k =p;
// 전반부, 후반부에 원소들을 하나씩 비교해 가며 tmp 배열에 담는다.
// 전반부와 후반부 배열 중 하나의 배열이 끝이 날 때 까지 탐색
while (i <= q && j <= r) {
if (data[i] <= data[j]) {
tmp[k++] = data[i++];
} else {
tmp[k++] = data[j++];
}
}
// 전반부에 남았 있는 데이터가 있으면 전부 담는다.
while (i <= q)
tmp[k++] = data[i++];
// 후반부에 남았 있는 데이터가 있으면 전부 담는다.
while (j <= r)
tmp[k++] = data[j++];
// data 에 tmp 값을 전부 담는다.
for (int a = p; a <= r; a++)
data[a] = tmp[a];
}
* 시간 복잡도

위 그림과 같이
T(n/2) + T(n/2) = 2 * T(n/2) => (대략) = n
T(n/2) + T(n/2) = 4 * T(n/4) => (대략) = n
..........
T(2) + T(2) + ... = n/2 * (2) = n
=> 따라서 n * (n이 2개 씩 다 나누어 떨어지는 갯수)
= n * log2n
의 시간 복잡도가 걸립니다.