Heap Sort (힙정렬)

* 특징
- 최악의 경우 시간 복잡도 O(nlogn)
- Sorts in place - 추가 배열 불필요
- 이진 힙 자료 구조를 사용
* 힙
1. Complete binary tree 이여야 한다.


- full binary tree : 모든 레벨에 노드들이 꽉 차있는 형태
- complete binary tree : 마지막 레벨을 제외하면 완전히 꽉 차있고, 마지막 레벨에는 가장 오른쪽 부터 연속된 몇개의 노드가 비어있을 수 있음
2. heap property를 만족 해야 한다.
- max heap property : 부모는 자식보다 크거나 같다
- min heap property : 부모는 자식보다 작거나 같다

* Heap의 표현
- 힙은 일차원 배열로 표현 가능 : A[1 . . n]
- 루트 노드 A[1]
- A[i]의 부모 = A[ i / 2 ]
- A[i]의 왼쪽 자식 = A[ 2i ]
- A[i]의 오른쪽 자식 = A[ 2i + 1 ]



* 연산 : max - heapify
- 전체를 힙으로 만들어라

* 연산을 진행 해보자


1. 먼저 루트의 서브 노드인 16 과 15가 자기 자신인 4보다 크니깐 Max heap property를 만족하지 않으므로
16, 15 중 더 큰 값인 16과 4를 exchange 해준다.
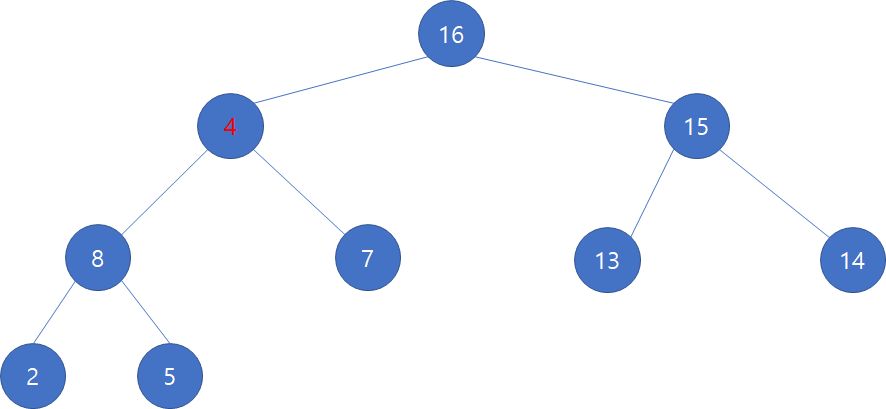

2. 그 다음으로 4와 8, 7은 Max heap property를 만족하지 않으므로 8, 7중 더 큰값인 8과 exchange 해준다.


3. 마지막으로 4와 2, 5 역시 heap property를 만족 시키기 위해서 5와 exchange를 시켜줍니다.
* SUDO 코드
MAX-HEAPIFY(A, i) {
if there is no child of A[ i ]
return;
k <- indoex of the biggest child of i;
if A[ i ] >= A[ k ]
return;
exchange A[ i ] and A[ k ];
MAX-HEAPIFY(A, k);
}MAX-HEAPIFY(A, i) {
while A[ i ] has a child do
k <- index of the biggest child of i;
if A[ i ] >= A[ k ]
return;
exchange A[ i ] and A[ k ];
i = k;
end
}
* 힙 만들기

1. [ 4, 1, 3, 2, 16, 9, 10, 14, 8, 7 ] 이 배열은 위 사진과 같은 Complete binary tree를 가지고 있다.
물론 Max heap property를 만족하지 못하기 때문에 heap 이 아니다.
heap으로 만들기 위해서 먼저 제일 마지막 노드의 부모 노드 A[ N / 2 ]를 max heapify 시킨다.
16의 자식 노드가 7 이기 때문에 따로 해줄 것이 없다.


2. 그다음으로 A[ N/2 - 1 ]를 Max heapify 시킨다.
2를 부모 노드로 가지고 14, 8이 자식 노드인 sub tree를 max heapify 시키면 14 - 2, 8 이 된다.


3. 위의 1번과 2번과 같은 방법으로 3을 max heapify 시킨다.
10 - 9, 3 으로 변경 된다.


4. 다음으로 1을 max heapify 한다.
16이 1과 exchange 되고, 1이 7과 exchange 된다.


5. 다음으로 4를 max heapify 한다.
4와 16이 exchange 되고, 4가 14와 exchange 되고, 4와 8이 exchange 된다.
6. heap 자료 구조가 완성된다.
* SUDO 코드
buildMaxHeap(A) {
for i = length(A)/2 down to 1
do maxHeapify(A, i)
}
* 힙 정렬 (heap sort)
1. 주어진 데이터로 힙을 만든다.
2. 힙에서 최대값(루트)을 가장 마지막 값과 바꾼다.
3. 힙의 크기가 1 줄어든 것으로 간주 한다. 즉, 가장 마지막 값을 반환해 주므로써 정렬이 이루어 진다.
4. 루트 노드에 대해서 heapify를 한다.
5. 정렬이 끝날 때 까지 반복 한다.
* SUDO 코드
heapSort( A ) {
buildMaxHeap( A ); // 힙 자료구조 생성
for i = heap_size down to 2 do // 힙 사이즈 부터 인덱스가 2까지 반복
exchange A[ 1 ], A[ i ]; // 마지막 노드와 루트 노드를 교환
heap_size = heap_size - 1; // 힙사이즈를 1 줄임
MaxHeapify(A, i); // heapify
}heapSort( A ) {
buildMaxHeap( A ); // 시간 복잡도 : n
for i = heap_size down to 2 do // 시간 복잡도 : n - 1
exchange A[ 1 ], A[ i ]; // 시간 복잡도 : 상수값
heap_size = heap_size - 1; // 시간 복잡도 : 상수값
MaxHeapify(A, i); // 시간 복잡도 : log2N
// 총 시간 복잡도 : n + 상수값 + (n-1)log2N
}