
* 탐색
그래프의 모든 노드들을 방문하는 일
* 대표적인 두 가지 방법
1. BFS : Breadth First Search, 너비 우선 탐색
2. DFS : Depth First Search, 깊이 우선 탐색
* DFS
맹목적 탐색 방법의 하나로 출발 노드로 부터 다음 레벨의 자식 노드를 탐색하고 또 그 다음 자식 노드를 탐색 하는 방법 입니다. 깊이를 우선으로 탐색 하는 방법 입니다.



1. 출발 노드에서 시작 합니다.
2. 현재 노드를 visited로 mark 하고 인접한 노드들 중 unvisited 노드가 존재하면 그 노드로 갑니다.
3. 2번을 계속 반복 합니다.
* DFS 동작 순서

위와 같은 그래프가 있을때 DFS로 탐색 한다면 아래 순서대로 노드를 방문 합니다.



① 출발노드1을 방문 합니다.
② 출발노드 1의 바로 자식 노드2를 방문 합니다.



③ 노드 4를 방문 합니다.
④ 노드 5를 방문 합니다.



⑤ 노드 6를 방문 합니다.
⑥ 노드 3를 방문 합니다.



⑦ 노드 8를 방문 합니다.
⑧ 노드 7를 방문 합니다.
* 총 노드 방문 순서 : 1 2 4 5 6 3 8 7
* 스택을 이용한 DFS 동작 순서
BFS에 경우에는 Queue에 FIFO(First In First Out) 속성을 이용해서 너비 우선에 탐색이 가능 합니다. DFS에 경우에는 반대로 Stack에 LIFO(Last In First Out) 속성으로 깊이 우선에 탐색이 가능 합니다.



① 출발노드1을 방문하고 노드 1의 이웃 노드 2와 3을 스택에 넣어 줍니다.



② 스택에 가장 마지막 노드 2를 출력하고 노드 2의 인접 노드 1, 4, 5를 스택에 넣어 주는데 노드 1은 이미 방문했다는 체크가 되어 있으므로 노드 4, 5만 스택에 넣어 줍니다.



③ 스택에 가장 마지막 노드 4를 스택에서 출력 하고 노드 4의 인접 노드 2를 스택에 넣어야 하는데 노드 2는 이미 방문 체크가 되어 있으므로 스택에 삽입 하지 않습니다.



④ 스택에 가장 마지막 노드 5를 출력 하고, 노드 5의 인접 노드 2, 3, 6을 스택에 삽입 합니다. 하지만, 노드 2와 노드 3은 이미 방문 체크가 되어 있으므로 노드 6만 삽입 합니다.



⑤ 스택에 가장 마지막 노드 6을 스택에서 출력 하고 노드 6의 인접 노드 5를 스택에 삽입 해야 하는데, 노드 5는 이미 방문 체크 되어 있으므로 아무것도 삽입 하지 않습니다.



⑥ 스택에 가장 마지막 노드 3을 스택에서 출력하고 노드 3의 인접 노드 1, 5, 8, 7을 스택에 삽입 하는데 노드 1, 5는 이미 방문 체크를 하였으므로 노드 8과 7만 삽입 합니다.



⑦ 스택에 가장 마지막 노드 8을 출력 하고 노드 8의 인접 노드 3을 스택에 삽입 하는데, 노드 3은 이미 방문 체크가 되었으므로 아무것도 삽입 하지 않습니다.



⑧ 스택에 가장 마지막 노드 7을 출력 하고 노드 7의 인접 노드 3을 삽입 하는데, 노드 3은 이미 방문 체크가 되어 있으므로 삽입 하지 않습니다.
스택이 비워 있으므로 DFS 탐색을 종료 합니다.
* 총 노드 방문 순서 : 1 2 4 5 6 3 8 7
* 재귀 함수를 이용한 DFS sudo 코드
앞에서 DFS는 Stack 자료구조를 활용하여 탐색 할 수 있다고 하였습니다.
Stack 자료구조를 직접 구현하거나 API를 사용 해도 되지만 대부분의 고급 프로그래밍 언어 에서 재귀 함수는 Stack 구조로 이루어져 있기 때문에 재귀 함수로 쉽게 DFS를 구현 할 수 있습니다.
DFS(G, V){
visited[ v ] ← YES;
for each node u adjacent to v do{
if visited[ u ] = NO then{
DFS(G, u);
}
}
}
* DFS를 반복하여 모든 노드를 방문 하는
sudo 코드 (disconnected node도 모두 방문)
DFS-ALL( G ){
for each v ∈ V
visited[ v ] ← NO; // 모든 노드를 no-visited노드로 초기화
for each v ∈ V
if (visited[ v ] = NO) then
DFS(G, V);
}
* DFS 시간 복잡도
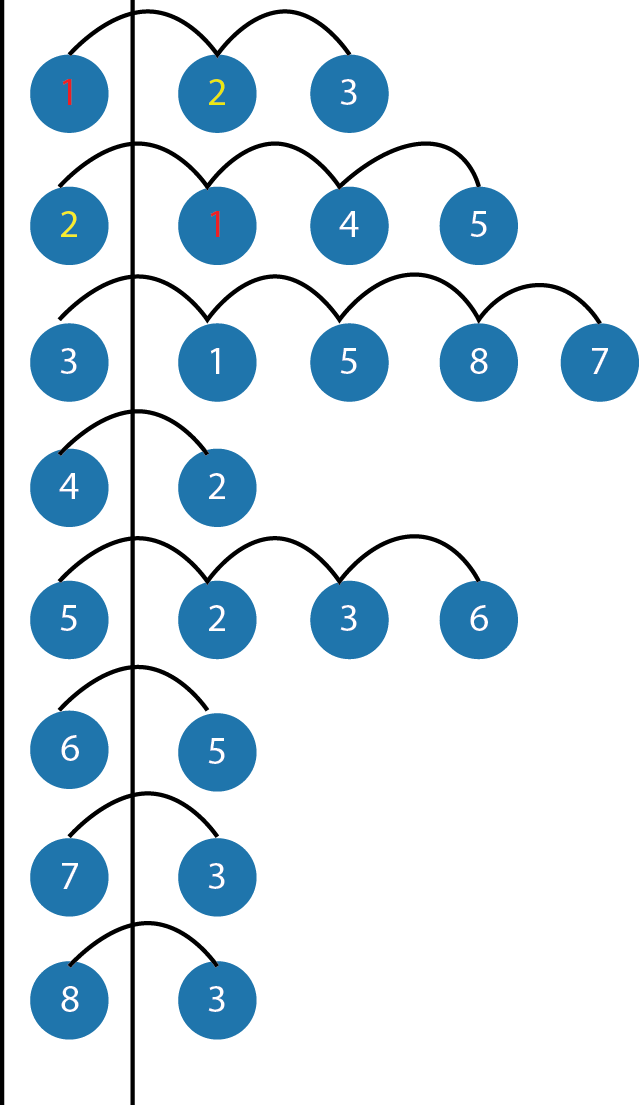

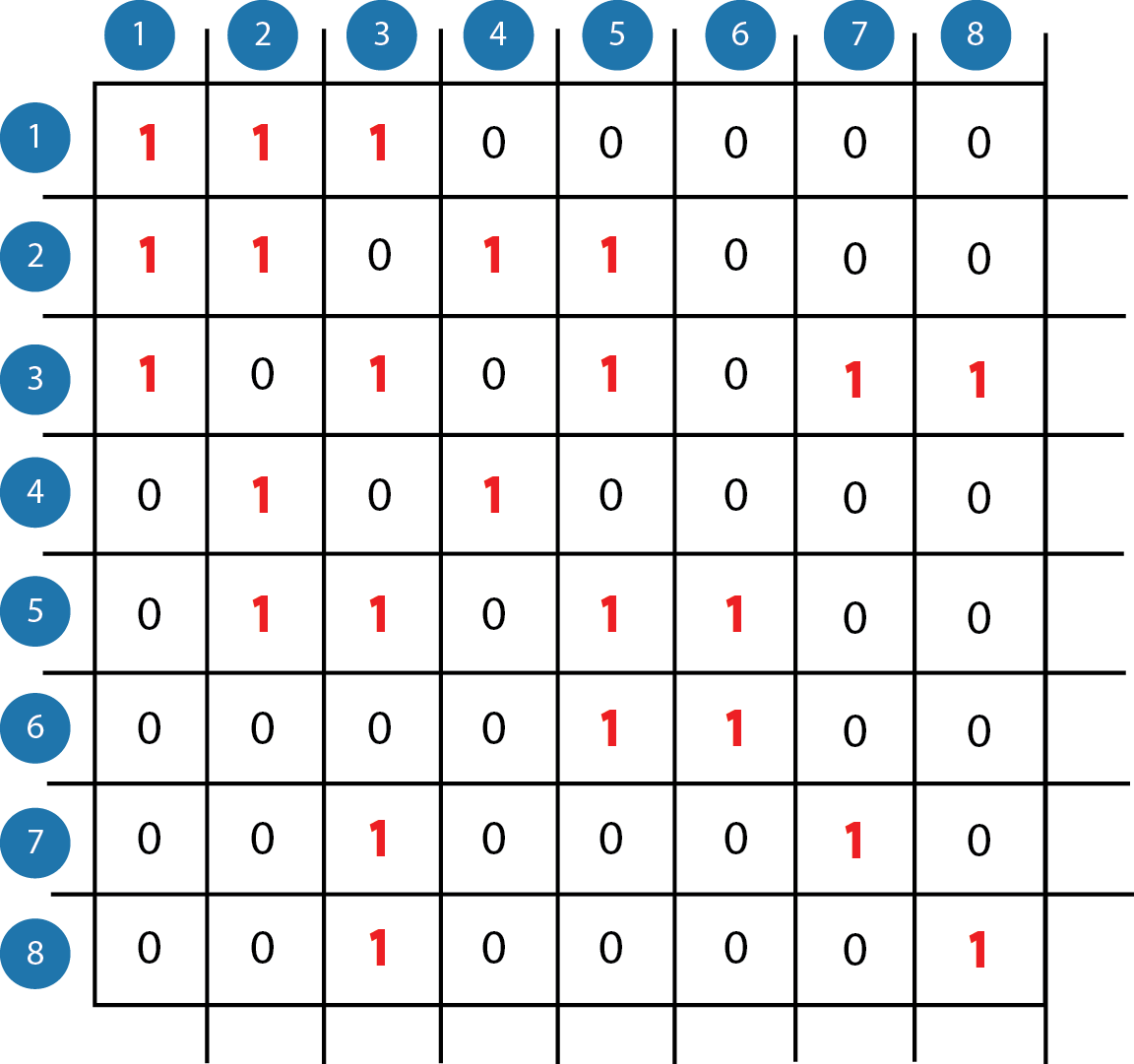
인접 리스트 인접 행렬
1. 인접 리스트로 구현 할 경우, 1차원 배열에 전체 노드가 중복 하지 않고 들어있고
각 노드에 대해서 인접한 노드들만이 인접리스트로 들어 있습니다. 그런데 무방향 그래프에서는 방향이 없기 때문에 1번 노드에서 2번 노드로 가는 엣지도 존재하고, 2번 노드에서 1번 노드로 가는 엣지도 존재 하기 때문에 2M (M: 엣지의 개수)의 시간 복잡도가 소요 됩니다.
2. 인접 행렬의 경우에는 2차원 배열로 어떤 한 노드의 인접 노드를 알기 위해서는
전체 노드를 모두 순회 해야 하기 때문에 노드의개수(N) * 노드의개수(N) = N2 만큼의 시간 복잡도가 소요 됩니다. 이때 인접 행렬에서 인접한 노드는 1로 인접하지 않은 노드는 0으로 표현 할 수 있습니다. 때문에 인접행렬에 자기 자신은 1로 표현 되어, 인접행렬의 대각선은 모두 1로 나타납니다.
* DFS vs BFS (미로 탐색)
BFS로 미로 탐색을 할 경우에는 갈림길 한 칸, 다른 길 한 칸,
이렇게 길 마다 조금씩 탐색을 진행 합니다.
하지만 DFS로 미로를 탐색 하는 경우는 갈림길이 나타나면 갈림길을 모두 탐색하여 길이 막혀 있음을 확인하고 다른 길로 향합니다.
여기서는 BFS가 도착지점 까지 더 빨리 도착 했지만, 미로에 생김새에 따라서 DFS가 더 빨리 도착 할 수도 있습니다.
또한 미로를 탐색 하는 중 갈림길에 존재하는 아이템을 줍는 기능 등의 따라 알고리즘의 선택을 다르게 할 수 있습니다.
'Algorithm' 카테고리의 다른 글
| LCA 최소 공통 조상 (0) | 2021.03.04 |
|---|---|
| BFS (Breadth First Search) 너비우선탐색 대해서 (0) | 2021.03.03 |
| Heap Sort (힙정렬) (0) | 2021.02.16 |
| 비트 마스크 (Bit Mask) (0) | 2021.02.01 |
| KMP 문자열 매칭 알고리즘 (0) | 2021.01.29 |