반응형

안녕하세요. 오늘 소개할 알고리즘은 다익스트라(Dijkstra) 알고리즘 입니다. 다익스트라(Dijkstra) 알고리즘은 흔히 어떠한 노드들 사이에서 출발 노드 부터 도착 노드 까지 최단 거리, 최단 경로를 찾는 알고리즘 입니다. 따라서, 가중치 그래프에서 사용할수 있는 알고리즘 입니다. 여기서 가중치는 거리라고 생각 하시면 되겠습니다.

위 그림 처럼 수원역에서 출발해서 강남역까지 최단 경로나 최단거리를 찾을때 사용 할 수 있는 알고리즘 입니다. 그럼 다익스트라(Dijkstra) 알고리즘의 핵심 아이디어를 한번 보시겠습니다.
1. 다익스트라(Dijkstra) 알고리즘 핵심 아이디어
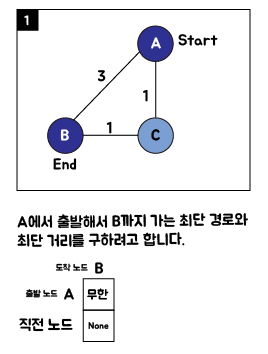
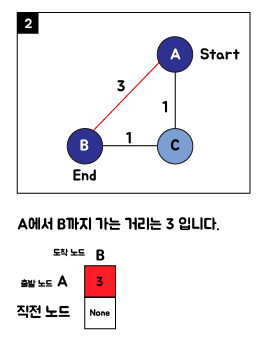
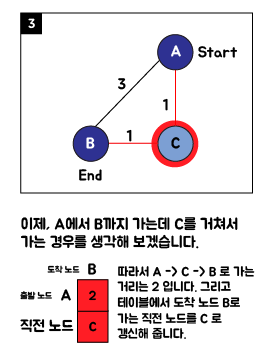
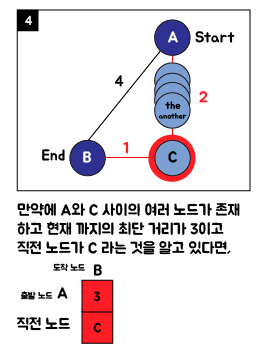
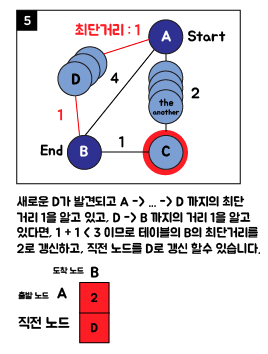
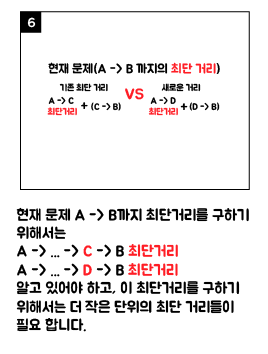


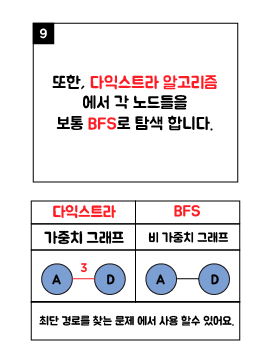
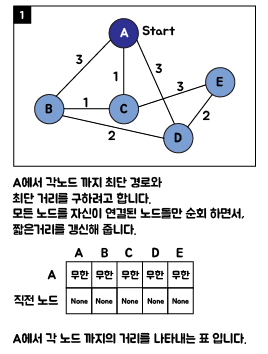
2. 다익스트라(Dijkstra) 알고리즘 순서도
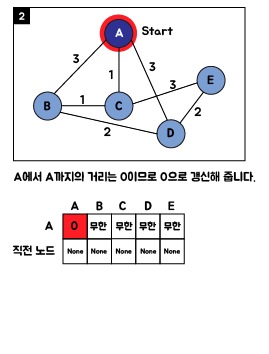
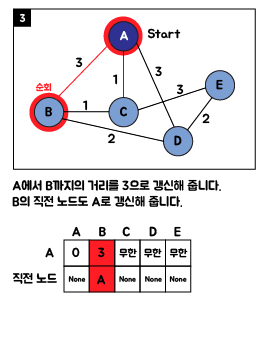
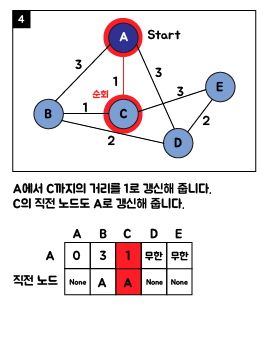
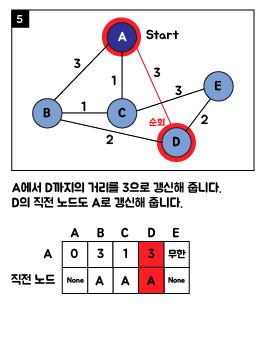
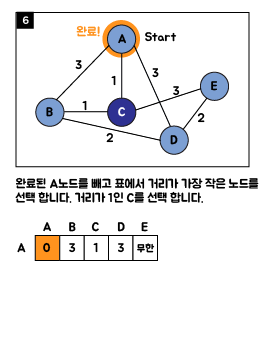
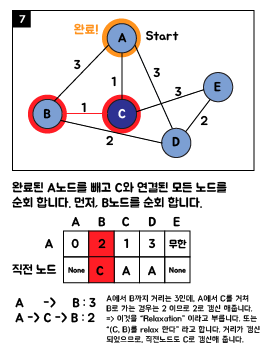
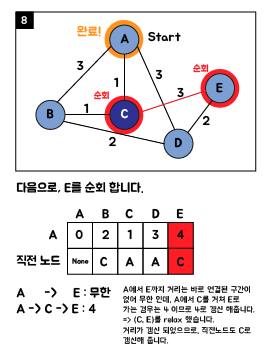
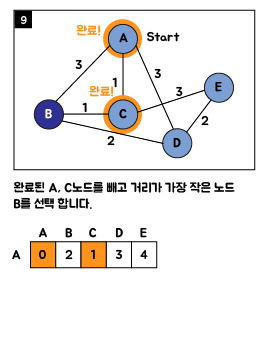
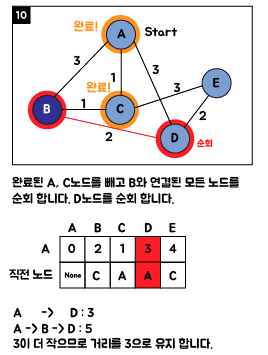
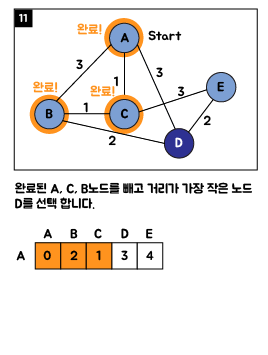
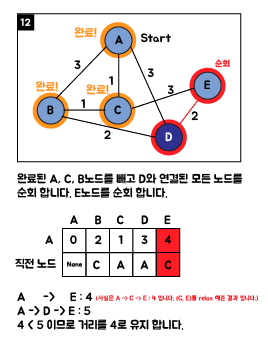
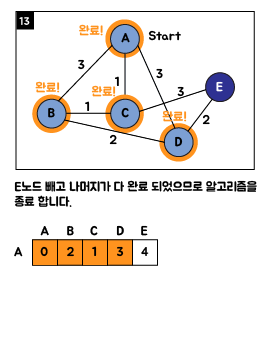
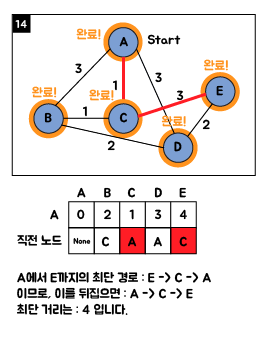

3. Java 소스 코드
public class DijkstraTest {
static final int INF = 100000000;
static final int num = 5;
public static void main(String[] args) {
// 방문한 노드 입니다.
boolean[] completed = new boolean[num];
// 결과로 출력할 최소 거리 배열 입니다.
int[] shortestDistance = new int[num];
// 전체 그래프를 초기화 합니다.
int[][] edge = {
{0, 3, 1, 3, INF},
{3, 0, 1, 2, INF},
{1, 1, 0, INF, 3},
{3, 2, INF, 0, 2},
{INF, INF, 3, 2, 0},
};
new ShortestPathFinder(completed, shortestDistance, edge, num, INF).dijkstra(0);
for (int i = 0; i < num; i++) {
System.out.printf("%d ", shortestDistance[i]); // 결과값 : 0 2 1 3 4 출력!
}
}
}
class ShortestPathFinder{
private int min;
private int num;
private boolean[] completed;
private int[] shortestDistance;
private int[][] edge;
ShortestPathFinder(boolean[] completed, int[] shortestDistance, int[][] edge, int num, int min){
this.completed = completed;
this.shortestDistance = shortestDistance;
this.edge = edge;
this.num = num;
this.min = min;
}
// 가장 최소 거리를 가지는 노드를 반환 합니다.
private int getSmallIndex() {
int index = 0;
for (int i = 0; i < num; i++) {
if (shortestDistance[i] < min && !completed[i]) {
min = shortestDistance[i];
index = i;
}
}
return index;
}
void dijkstra(int start) {
for (int i = 0; i < num; i++)
shortestDistance[i] = edge[start][i];
completed[start] = true;
for (int i = 0; i < num - 2; i++) {
int current = getSmallIndex();
completed[current] = true;
for (int j = 0; j < num; j++) {
if (!completed[j]) {
if (shortestDistance[current] + edge[current][j] < shortestDistance[j]) {
shortestDistance[j] = shortestDistance[current] + edge[current][j];
}
}
}
}
}
}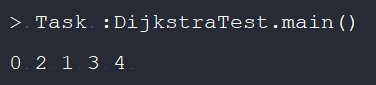
위에서 설명한 노드와 거리 값들을 입력해 주고 출력 시켜보면 0 2 1 3 4 의 해당하는 최단 거리값들이 출력 되는 것을 알수 있습니다.
하지만, 위와 같은 소스 코드는 이중 반복문이 사용되어 시간 복잡도가 O(N^2) 으로 오래 걸리고 비효율적 입니다. 따라서 이 시간 복잡도를 줄이기 위해서 다음과 같이 구현하여 시간 복잡도를 줄일수 있습니다.
힙(heap)을 이용한 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘 안녕하세요. 오늘 소개할 알고리즘은 다익스트라(Dijkstra) 알고리즘 입니다. 다익스트라(Dijkstra) 알고리즘은 흔히 어떠한 노드들 사이에서 출발 노드 부터 도착 노드
coding-food-court.tistory.com
반응형
'Algorithm' 카테고리의 다른 글
| 미로 탈출 문제 (0) | 2020.08.29 |
|---|---|
| 카카오 가사 검색 문제(Trie 트리) (0) | 2020.08.28 |
| 이진 탐색(Binary Search) (0) | 2020.08.27 |
| 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2020.08.25 |
| 힙(heap)을 이용한 다익스트라(Dijkstra) 알고리즘 (0) | 2020.08.13 |