문제 설명
크기가 N인 덱(deque)이 주어지고, 덱의 첫 번째 위치는 1, 덱의 마지막 위치는 N으로 지정합니다. 이때, 덱에서 M개의 수를 뽑아내려고 합니다. 뽑아내는 순서가 주어질 때, 뽑아내는 과정에서 덱이 최소로 회전하는 횟수를 구하는 문제입니다.
이때 덱은 아래 3가지 연산만 할 수 있습니다.
- (f1연산) 첫번째 원소를 뽑는다. {a1…ak} → {a2…ak}
- (f2연산) 왼쪽으로 한칸 이동. {a1…ak} → {a2…ak, a1}
- (f3연산) 오른쪽으로 한칸 이동. {a1…ak} → {ak, a1…ak-1}
동작
graph TD;
Start[시작] --> Input[입력];
Input --> InitQueue[덱 자료구조 초기화];
InitQueue --> Loop[루프 시작];
Loop --> Check[뽑아내려는 수의 위치 찾기];
Check --> |앞쪽인 경우| RotateFront[앞쪽으로 회전시키기];
Check --> |뒤쪽인 경우| RotateRear[뒤쪽으로 회전시키기];
RotateFront --> |뽑아내기| RemoveElement[원소 제거];
RotateRear --> |뽑아내기| RemoveElement;
RemoveElement --> |모든 수를 뽑아내었는지 확인| End[종료];
End --> Output[출력];
java 코드
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;
public class BOJ1021_2 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int result = 0;
Deque<Integer> deque = new ArrayDeque<>(N);
for (int i = 0; i < N; i++) {
//index로 deque를 채운다.
deque.add(i + 1);
}
int[] indices = new int[M];
for (int i = 0; i < indices.length; i++) {
indices[i] = sc.nextInt();
}
for (int index : indices) {
//뽑아내려는 수의 위치 찾기
//deque의 첫번째값 ~ index 까지 거리 구하기
int headToIndex = 0;
for (int j : deque) {
if (index == j) {
break;
}
headToIndex++;
}
int tailToIndex = deque.size() - headToIndex - 1;
if (headToIndex <= tailToIndex) {
//앞쪽으로 회전
while (deque.getFirst() != index) {
deque.addLast(deque.pollFirst());
result += 1;
}
} else {
//뒤쪽으로 회전
while (deque.getFirst() != index) {
deque.addFirst(deque.pollLast());
result += 1;
}
}
//원소 제거
deque.removeFirst();
}
System.out.println(result);
}
}
어려웠던 부분
f2, f3연산을 최소로 하기 위해서는 주어진 인덱스 값을 deque의 head와 가까우면 f2 연산을 진행하고, tail과 가까우면 f3연산을 진행해서 deque 값을 넣어보고 시뮬레이션 돌리는 방법으로 구현하면 되는듯 싶었다.
그러나, deque을 회전을 시키면서, head값과 tail값이 달라지기 때문에 head, tail에 가까운지 계산하는 부분이 헷갈렸다. 처음에는 head와 tail 값을 뽑아서 비교해보는 식으로도 진행을 했지만, 값을 뽑아보아도 head와 tail 사이에 어떤 값이 들어가있는지는 알수가 없었다.
따라서, 회전을 하기 전에, headToIndex 값을 미리 구하고, 구한 headToIndex 값과 deque.size()값을 이용해서 tailToIndex 를 구하는 로직으로 수정하였다. 이 내용을 구현한 부분이 아래 로직이다.
//뽑아내려는 수의 위치 찾기
//deque의 첫번째값 ~ index 까지 거리 구하기
int headToIndex = 0;
for (int j : deque) {
if (index == j) {
break;
}
headToIndex++;
}
int tailToIndex = deque.size() - headToIndex - 1;
덱(deque) 자료구조
덱(deque) 자료구조는 큐(queue)와 스택(stack)의 특징을 모두 가지고 있는 자료구조입니다. 내부적으로 deque은 double-linked list로 구현되어 있습니다. 그래서 양 끝의 요소의 추가/삭제가 O(1)을 만족하게됩니다.
덱(deque) 자료구조 연산자
위 자바 소스코드를 보면, 아래 구문이 있다.
//앞으로 회전
deque.addLast(deque.pollFirst());
//뒤로 회전
deque.addFirst(deque.pollLast());
여기서, 처음에 저는 deque.pollFirst() 대신에 deque.removeFirst()를 사용했다.
- pollFirst() : 덱의 앞쪽에서 원소를 제거하고, 해당 원소를 반환. 덱이 비어있으면 null을 반환.
- removeFirst() : 덱의 앞쪽에서 원소를 제거하고, 해당 원소를 반환. 덱이 비어있으면 예외가 발생
앞 원소를 반환하는거는 같지만, 덱이 비어있을때, 처리하는 방식이 다르다. 이처럼 덱(deque)은 스택과 큐 구조를 동시에 가지고 있기 때문에, 헷갈리는 메소드들이 많다. 아래 그림을 참고하자.
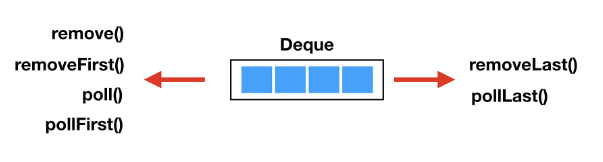
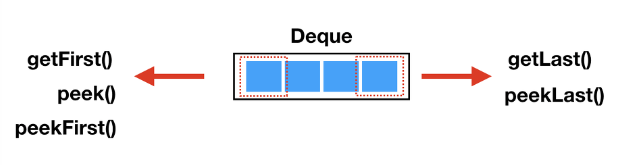
덱 자료구조를 활용한 문제 해결 방법의 장점
덱 자료구조를 활용하여 문제를 해결하는 방법은 다음과 같은 장점이 있습니다.
- 시간 복잡도가 낮습니다.
- 코드가 간결해집니다.
- 구현하기 쉽습니다.
덱 자료구조를 활용하면 시간 복잡도를 낮출 수 있기 때문에, 대용량의 데이터를 처리할 때 유용합니다. 또한, 덱 자료구조를 이용하면 코드가 간결해지기 때문에, 가독성이 좋아집니다. 또한, 구현하기 쉬우므로 코딩 테스트에서도 유용하게 사용할 수 있습니다.
결론
덱 자료구조는 큐와 스택의 장점을 모두 가지고 있기 때문에, 다양한 알고리즘에서 유용하게 사용됩니다. 덱 자료구조를 활용하여 문제를 해결하는 방법은 시간 복잡도를 낮출 수 있기 때문에, 대용량의 데이터를 처리할 때 유용하며, 코드가 간결해지기 때문에 가독성이 좋아집니다. 또한, 구현하기 쉬우므로 코딩 테스트에서도 유용하게 사용됩니다.
'Algorithm' 카테고리의 다른 글
| 피보나치 수열 (재귀 vs 비재귀) (0) | 2023.06.17 |
|---|---|
| 2개의 json key 값을 비교하는 방법 (0) | 2023.06.10 |
| display flex5, align-items align-content , 아이템 정렬 방법 (0) | 2021.03.17 |
| 접두사, 접미사를 이용한, KMP 문자열 매칭 알고리즘 2 with Java (0) | 2021.03.16 |
| KMP 문자열 매칭 알고리즘 vs 순차 탐색 알고리즘 (0) | 2021.03.15 |