반응형
아래는 피보나치 수열입니다.
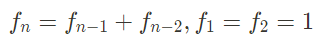
1. 재귀 버전
이는 재귀 알고리즘으로 아래와 같이 구현 할수 있습니다.
fib(n):
if (n = 1 or n = 2)
return 1
else
return fib(n - 1) + fib(n - 2)이는 재귀 알고리즘으로 구현한 치명적인 예 입니다. 시간이 너무 오래 걸립니다. 100번째 피보나치 수를 계산하기 위해서 fib(100)을 수행하면 평생 기다려도 결과를 볼 수 없습니다.
이렇게 엄청난 시간이 걸리는 이유는 한번 계산해 놓은 결과를 계속 호출하여 지수함수적인 중복을 일으키기 때문이다.
이 문제를 다음과 같이 수정하여 fib2(100)은 어마어마하게 시간을 단축 시킵니다.
2. 비재귀 버전
fib2(n) :
f[1] ← f[2] ← 1 //f[2] ← 1과 f[1] ← 1 을 한꺼번에 적어놓은 것
for i ← 3 to n
f[i] ← f[i-1] + f[i-2]
return f[n]재귀는 문제를 해결하는 유용한 도구이지만 잘못 쓰면 치명적일수 있습니다.
반응형
'Algorithm' 카테고리의 다른 글
| 2개의 json key 값을 비교하는 방법 (0) | 2023.06.10 |
|---|---|
| [백준 1021] 회전하는 큐 (1) | 2023.02.25 |
| display flex5, align-items align-content , 아이템 정렬 방법 (0) | 2021.03.17 |
| 접두사, 접미사를 이용한, KMP 문자열 매칭 알고리즘 2 with Java (0) | 2021.03.16 |
| KMP 문자열 매칭 알고리즘 vs 순차 탐색 알고리즘 (0) | 2021.03.15 |