
1. 투포인터(Two Pointer)
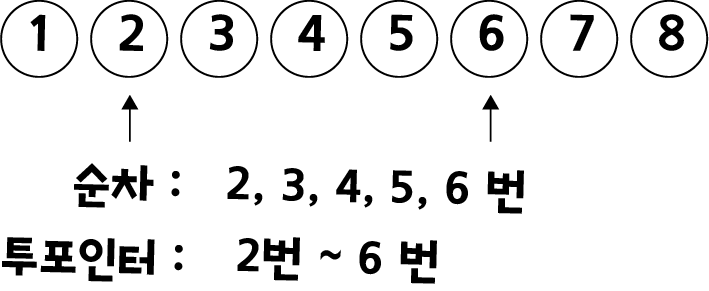
1번 부터 8번 까지의 공이 존재 할때, 그 중 2, 3, 4, 5, 6번 순차적으로 접근해야 할 경우, 시작 점, 끝 점 으로 편하게 데이터를 나타낼 수 있습니다.

만약, 부분합이 3이 되는 연속 수열의 갯수를 찾아야 한다면, 위 그림과 같이 찾는 값이 부분합 보다 크다면, 끝 인덱스를 1 증가 시켜 데이터의 범위를 증가 시키고, 찾는값이 부분합 보다 작거나, 같다면 시작 인덱스를 1 증가 시켜 데이터의 범위를 감소 시켜, 찾는 값의 가까워지도록 탐색 할수 있습니다. 단, 이 경우 수열의 모든 값은 양의 정수 이어야 합니다. 이러한 원리를 이용해서 1, 2, 3, 4로 이루어진 배열의 부분합이 3이 되는 경우의 수를 모두 구해 보겠습니다.
2. 부분 합이 3이 되는 경우의 갯수 구하기
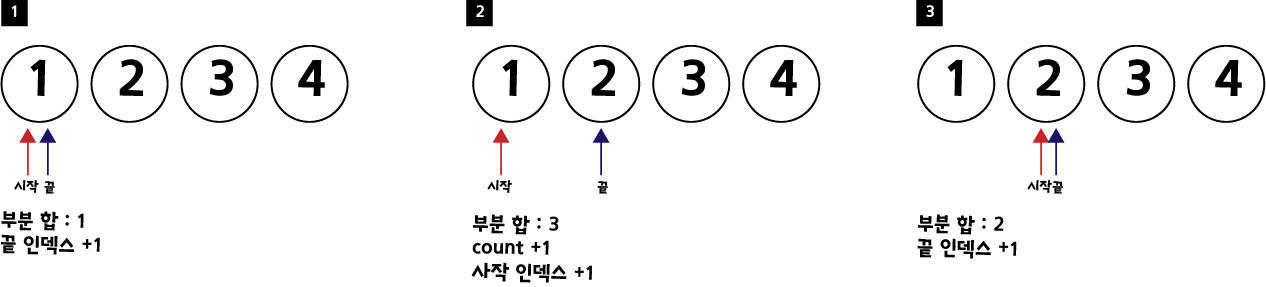
순서 2번의 경우 1 + 2 = 3으로, 부분합 3을 찾았으므로, count를 1증가 시켜 주겠습니다.
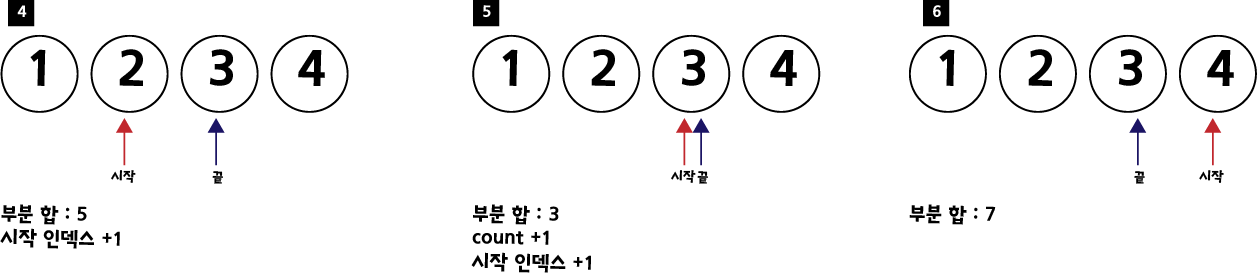
순서 5번의 경우, 부분 합이 3이므로, count를 1증가 시켜 주겠습니다.

따라서, 위 수열에서 부분합이 3이 되는 경우는 총 2번 입니다.
3. 부분합 경우의 수 java 소스 코드
/*
* 양의 정수로 이루어진 수열에서
* 부분 합을 시작 포인터와 끝 포인터 의 범위를 조정 하며
* 찾을 수 있습니다. (Merge Sort 에서 활용)
* */
public class TwoPointer {
public static void main(String[] args) {
int n = 4; // 데이터의 갯수
int m = 3; // 찾고자 하는 부분합
int[] arr = {1, 2, 3, 4}; // 전체 수열
int cnt = 0; // 부분합의 갯수
int intervalSum = 0; // 부분합
int end = 0; // 끝 인덱스
// start를 차례대로 증가시키며 반복
for (int start = 0; start < n; start++) {
// end를 가능한 만큼 이동시키기
while(intervalSum < m && end < n) {
intervalSum += arr[end];
end += 1;
}
// 부분합이 m일 때 카운트 증가
if (intervalSum == m) {
cnt += 1;
}
intervalSum -= arr[start];
}
System.out.print(cnt);
}
}출력 결과

4. 두 정렬된 배열을 하나의 정렬된 배열로 합치기
정렬 된 두 배열 A, B가 주어졌을 때
A 배열의 인덱스 : i
B 배열의 인덱스 : j
결과 배열의 인덱스 : k
입니다. 이 때
if (A[i] < B[j])
then '결과배열[k]' = A[i]; i++;
else
then '결과배열[k]' = B[j]; j++;
이런 원리로 결과 배열을 모두 채워 줍니다.

(1 < 2) 이므로, 결과 배열의 1을 채워 줍니다. (3 > 2) 이므로, 결과 배열의 2를 채워 줍니다.

(4 > 3) 이므로, 결과 배열의 3을 채워 줍니다. (6 > 5) 이므로, 결과 배열의 5를 채워 줍니다.
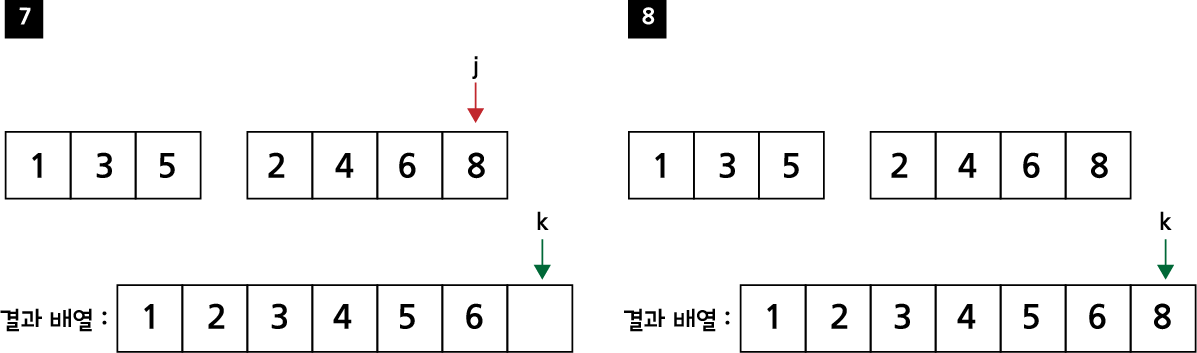
인덱스 i를 끝까지 채웠으므로, 나머지 인덱스 j의 값도 순서대로 모두, 인덱스 k의 채워 주면 되겠습니다.
5. 정렬된 두 배열 하나의 배열로 함치기 java 소스 코드
/*
* 정렬된 두 배열을
* 하나의 정렬된 배열로 합치기 위해서
* Two Pointer 를 이용합니다. (Merge Sort 에서 활용)
* */
public class TwoPointerMerge {
public static void main(String[] args) {
int[] a = {1, 3, 5};
int[] b = {2, 4, 6, 8};
int n = a.length;
int m = b.length;
// 결과 배열 초기화
int[] result = new int[n + m];
// i는 A인덱스, j는 B인덱스, k는 결과배열 인덱스
int i = 0, j = 0, k = 0;
// 배열 a, b는 각각 정렬 되어 있음
while (i < n && j < m) {
if (a[i] < b[j])
result[k++] = a[i++];
else
result[k++] = b[j++];
}
// 비어있는 k의 나머지 모두 넣어 주기
while (i < n) result[k++] = a[i++];
while (j < m) result[k++] = b[j++];
for (int e : result) {
System.out.printf("%d ", e);
}
}
}출력 결과
이와 같이, 알고리즘을 구현하면, 시간 복잡도는 O(N + M) 으로, N : 배열 A의 크기, M : 배열 B의 크기에 해당 합니다. 투 포인터(Two Pointer)를 이용한 '정렬된 두배열 합치기' 는 Merge Sort(병합 정렬) 의 merge 하기 위해서 사용 됩니다.
배열 합치기 - '백준 11728번'
11728번: 배열 합치기 첫째 줄에 배열 A의 크기 N, 배열 B의 크기 M이 주어진다. (1 ≤ N, M ≤ 1,000,000) 둘째 줄에는 배열 A의 내용이, 셋째 줄에는 배열 B의 내용이 주어진다. 배열에 들어있는 수는 절��
coding-food-court.tistory.com
'Algorithm' 카테고리의 다른 글
| 감시 피하기 - '백준 18428번' (0) | 2020.10.11 |
|---|---|
| 구간 합 구하기 알고리즘 (0) | 2020.10.07 |
| 순열 알고리즘 (0) | 2020.10.02 |
| 조합 알고리즘 (0) | 2020.09.30 |
| 고정점 찾기 - 이것이 코딩 테스트다 with java (0) | 2020.09.24 |