반응형

1. 문제

위와 같은 배열이 주어지고, 쿼리 : (left 인덱스, right 인덱스) 가 주어졌을 때, 이 쿼리는 left 인덱스 부터 right 인덱스 까지 수의 합을 반환해야 합니다. 이때 쿼리는 총 M(1 <= M <= 1,000,000)개 이고, 배열의 개수는 N(1 <= N <= 1,000,000) 입니다. 이때, 주어진 M개의 쿼리가 반환한 값을 모두 출력 하시오.
2. 접근
배열의 개수도 최대 백만, 쿼리의 개수도 최대 백만 입니다. 이 쿼리를 순차 탐색으로 모두 진행하면 시간 복잡도는 O(NM) = (1,000,000 x 1,000,000 = 1조) 이 되겠습니다. 따라서, 순차 탐색으로는 문제를 풀지 못할 것 입니다.
따라서, 다음과 같이 접근 합니다.
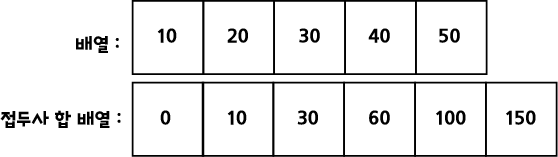
1. 배열 N개 모두에 대해서 접두사 합(Prefix Sum)을 '새로운 배열'의 저장해 둡니다. (시간 복잡도 : O(N))
2. 쿼리 : (L, R) 을 구할때는, '새로운 배열[R]' - '새로운 배열[L - 1]' 공식으로 구할 수 있습니다. (시간 복잡도 : O(1))
3. 따라서, 전체 쿼리 M개에 대한 시간 복잡도 : O(N + M) 입니다.
3. 구간 합 java 소스 코드
/*
* 배열의 구간 합을
* 접두사 합(Prefix Sum)을 구해서
* 시간 복잡도 O(N + M(쿼리의개수)) 만의 구할수 있다.
* */
public class SumOfInterval {
int[] arr;
int n;
int[] prefixSumArr;
public static void main(String[] args) {
int[] arr = {10, 20, 30, 40, 50};
SumOfInterval sumOfInterval = new SumOfInterval(arr);
// 예를 들어, 배열 (3, 4) 구간 합을 계산 하기
int left = 3;
int right = 4;
System.out.print(sumOfInterval.query(left, right));
}
public SumOfInterval(int[] arr) {
this.arr = arr;
this.n = arr.length;
this.prefixSumArr = new int[n + 1];
// 입시 합
int tmpSum = 0;
// 접두사 합 배열 만들기
int i = 1;
for (int val : arr) {
tmpSum += val;
prefixSumArr[i++] = tmpSum;
}
}
public int query(int left, int right) {
return prefixSumArr[right] - prefixSumArr[left - 1];
}
}출력 결과

반응형
'Algorithm' 카테고리의 다른 글
| 백준 18352번 - '특정 거리의 도시 찾기' (0) | 2020.10.16 |
|---|---|
| 감시 피하기 - '백준 18428번' (0) | 2020.10.11 |
| 투 포인터(Two Pointer) 알고리즘 (0) | 2020.10.07 |
| 순열 알고리즘 (0) | 2020.10.02 |
| 조합 알고리즘 (0) | 2020.09.30 |